Orbit Calculator: Calculate Orbital Velocity, Period and Eccentricity

About this 'Orbit Calculator'

This complete Orbit Calculator provides a set fast and reliable calculations:

• Orbital velocity calculator
• Orbit period calculator
• Orbit eccentricity calculator

The Orbital Calculator package is an essential tool for calculating the orbital velocity and period of a spacecraft in both circular and elliptical orbits around the Earth. It is intended for engineers working in mission planning, spacecraft design, or orbital analysis. The tool uses core orbital mechanics equations to estimate key parameters based on inputs like radius, mass, and altitude. It supports standard unit inputs and is suitable for feasibility assessments before deeper simulation.

• Aerospace Engineers designing satellite trajectories or interplanetary missions.
• Astrophysics Researchers and Students modeling real-world orbital conditions.
• Mission Planners needing quick parameter checks for various orbital configurations.

The Orbital Mechanics Calculator allows for quick feasibility checks to evaluate how changes in apogee, perigee, or orbit type affect the spacecraft’s velocity and orbital period. Users can enter parameters such as mass, radius, or orbital height to perform calculations related to orbital velocity and period. While some softwares can provide advanced simulation capabilities, this tool offers a streamlined approach for initial design and analysis.

For further reading and in-depth understanding, refer to:

• Fundamentals of Astrodynamics by Bate, Mueller, and White
• Orbital Mechanics for Engineering Students by Howard D. Curtis

Understanding Orbital Parameters

Understanding orbital parameters is fundamental to modeling the motion of celestial bodies—such as planets, moons, and satellites—as they orbit around a larger object like the Sun or Earth. These parameters, which include the semi-major axis, eccentricity, and the gravitational constant, define the size, shape, and dynamics of an orbit. In scientific literature, orbital parameters are typically expressed in standard units: kilometers for distances like radius or semi-major axis, and kilograms for mass. For example, the semi-major axis of Mars’ orbit around the Sun is about \(227.9\) million kilometers, a value that helps determine both the orbital period and speed of Mars as it travels through space. The gravitational constant, denoted as \(G\), is a universal value that quantifies the strength of gravitational attraction between objects. In the case of Earth’s orbit around the Sun, these parameters allow scientists and engineers to accurately model and predict the planet’s path, speed, and period. By understanding and applying these orbital parameters, we can analyze the orbits of other planets, satellites, and even asteroids.

Orbital Speed and Trajectory

The orbital speed of a celestial body is directly influenced by its distance from the center of the larger object it 9orbits. In elliptical orbits, two key points—apogee (the farthest point) and periapsis (the closest point)—play a significant role in determining both the speed and trajectory of the orbiting object. The standard gravitational parameter, represented by μ, is central to calculating orbital speed and period. For example, in a circular orbit around Earth, the orbital speed can be determined using the formula: velocity \(= \sqrt{\frac{\mu}{\text{radius}}}\), where \(μ\) is the standard gravitational parameter for Earth and the radius is the distance from Earth’s center to the satellite. The Moon’s orbit around Earth is a classic case of an elliptical orbit, with an apogee of about \(405,500\) kilometers and a periapsis of roughly 363,300 kilometers, resulting in varying speeds at different points along its path. By entering the mass of the central body and the radius of the orbit into a calculator, you can quickly determine the orbital speed and trajectory for any celestial body, whether it’s a satellite in low Earth orbit or a spacecraft traveling to other planets.

FAQs

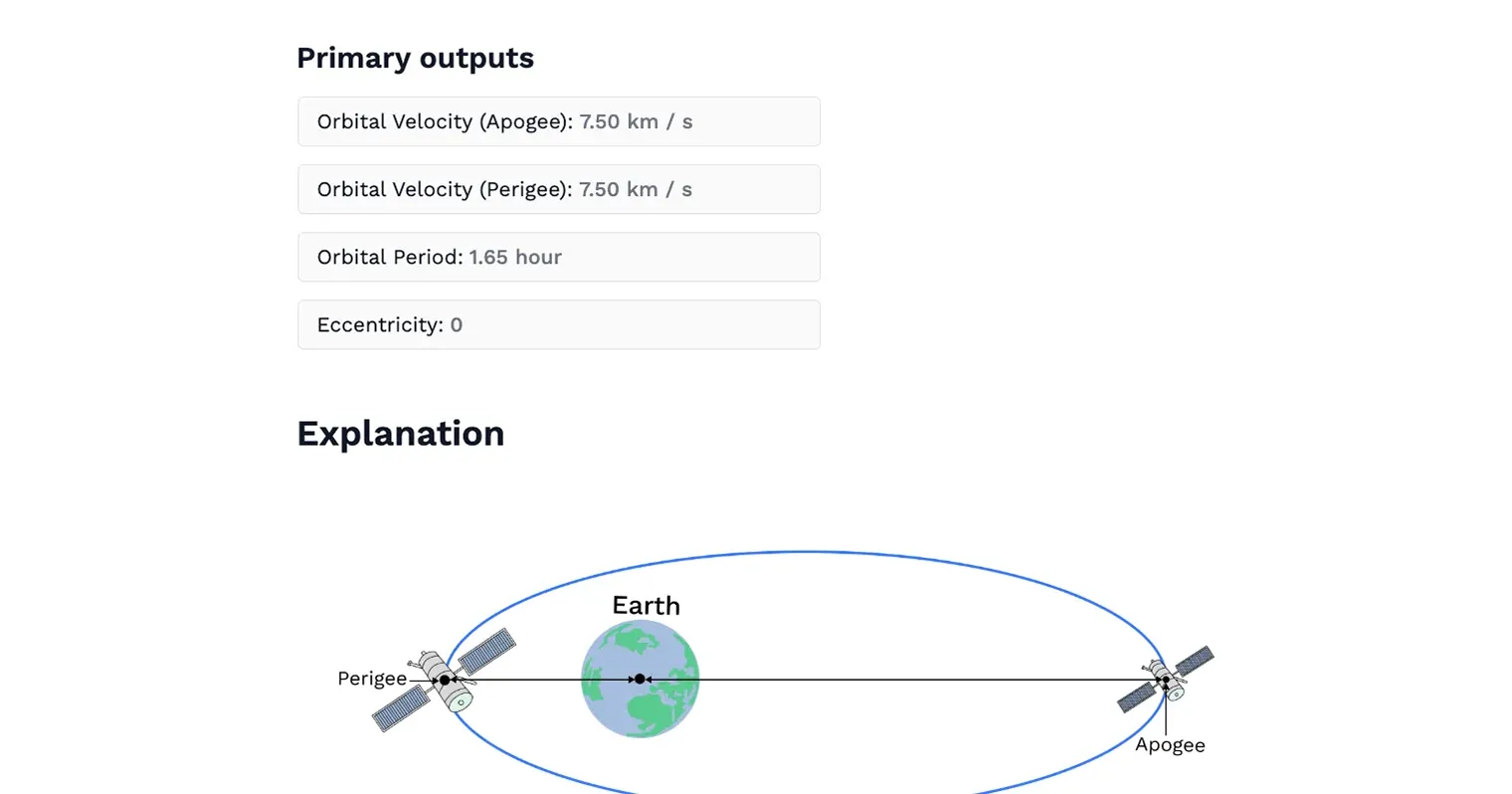
How does the apogee and perigee affect orbital velocity and period?

The apogee (farthest point) and perigee (closest point), also known as apoapsis and periapsis in orbital mechanics, determine the spacecraft’s speed and orbital duration, with elliptical orbits having varying velocities at different points. The distance from the center of the planet or other celestial body, including the height above the surface, is a key parameter in these calculations. For example, the Moon’s orbit around Earth has an apogee (apoapsis) at a specific height above Earth's surface. The orbital period is the time it takes for a moon, planet, or asteroid to complete one orbit. When calculating orbital speed, the standard gravitational parameter μ and the gravitational constant \(G\) are used, with mass measured in \(kg\). The orbital energy involved is large, on the order of \($$10^{33}$$\) J for planets. These principles apply to the orbits of various celestial bodies, including asteroids, planets, and moons.

How can orbital period be useful for mission planning?

The orbital period helps determine how long it takes for a spacecraft to complete one orbit, which is essential for timing communication, Earth observations, or docking maneuvers.

The answer for the orbital period can be derived using Kepler's third law and related equations.

What alternative tools can be used for orbital mechanics calculations?

Software like GMAT, STK, or Python libraries such as Poliastro and PyEphem can provide detailed simulations and additional insights into orbital dynamics. You can use those Python libraries on CalcTree too!

How to verify a calculation

Engineering calculations require clarity, precision, and professionalism. Here are some best practices we use at CalcTree:

• Technical Requirements: Start with boundary conditions, units, sign conventions, and design standards.
• Check the Math: Review the calculation step-by-step. Clarify unusual steps, compare results with hand calculations or tools, and test with multiple examples.
• Peer Review: Have an independent reviewer check for logic, accuracy, and compliance.

For more on verification, see CalcTree’s internal methods.