Free Beam Analysis Pack using Macaulay's Theorem Calculator. Step-by-step, engineering-grade tool with downloadable report.

This template is not available yet. You can sign up and create it yourself!
Or let us know if you'd like to be notified when it’s ready:
About this Beam Analysis using Macaulay's Theorem Calculator
The Beam Analysis pack using Macaulay's Theorem is a specialized tool for determining shear force, bending moment, and deflection in a single-span beam under various types of applied loading. The tools are designed to analyze simply supported beams and cantilever beams, offering valuable insights for structural analysis and design. It’s ideal for:
- Structural engineers needing precise deflection and bending moment calculations for simply supported beams or cantilever beams.
- Civil engineers checking how point load, distributed loads, or multiple point loads impact performance.
- Educators and students looking for a reliable tool to learn and verify solutions from beam theory.
The pack includes the following designs:
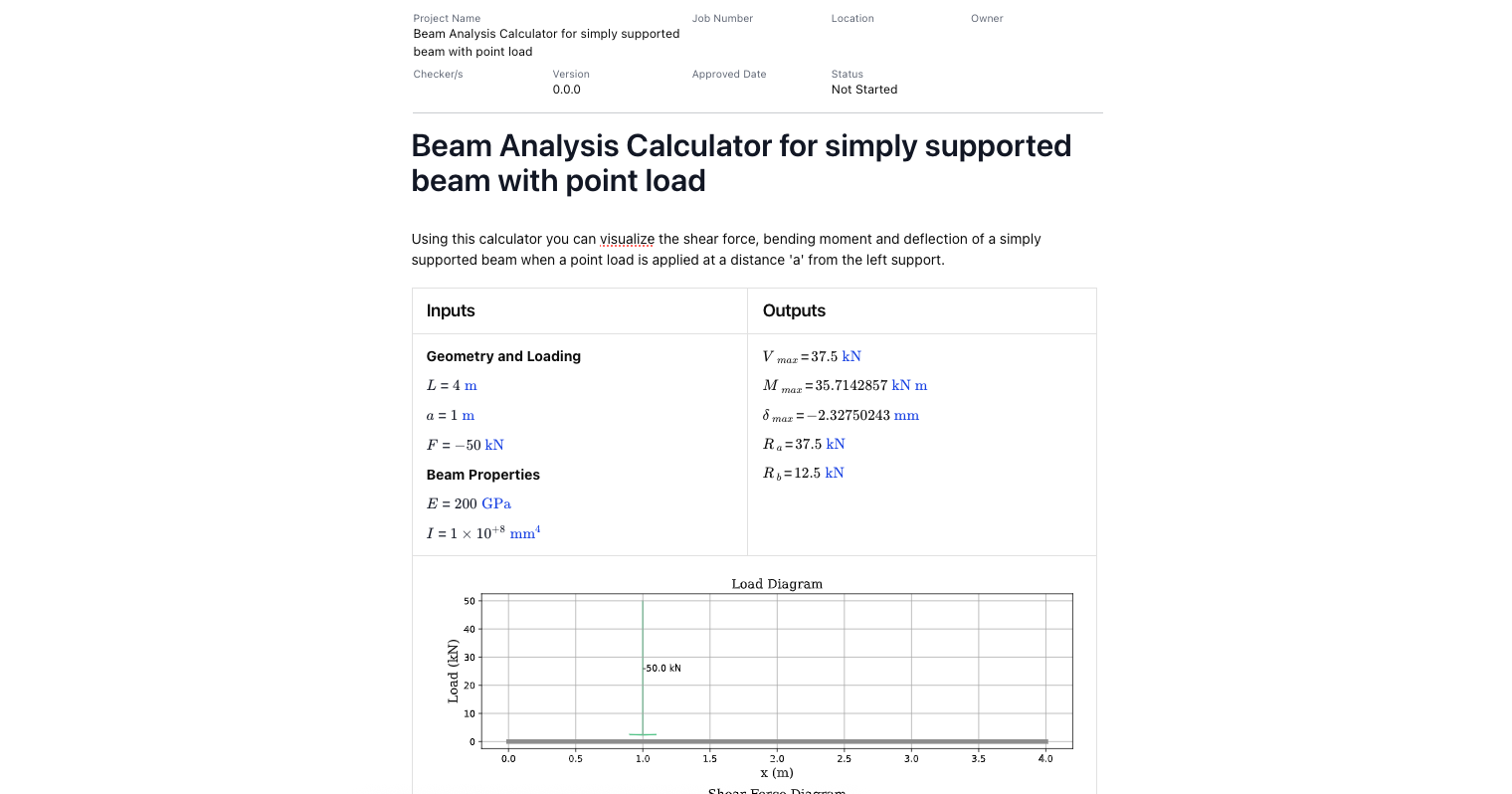
- Simply supported beam with point load
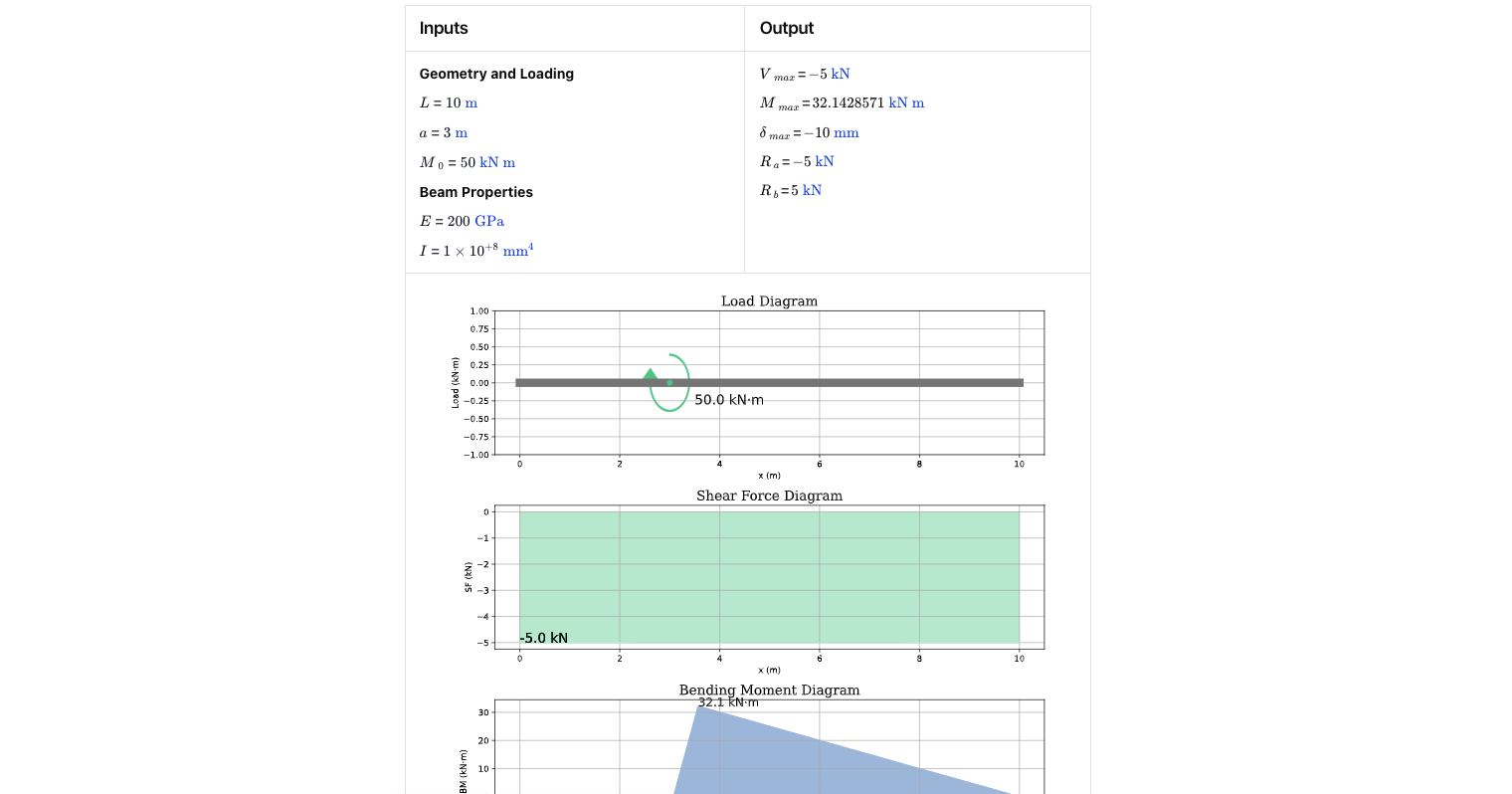
- Simply supported beam with point moment
- Simply supported beam with UDL
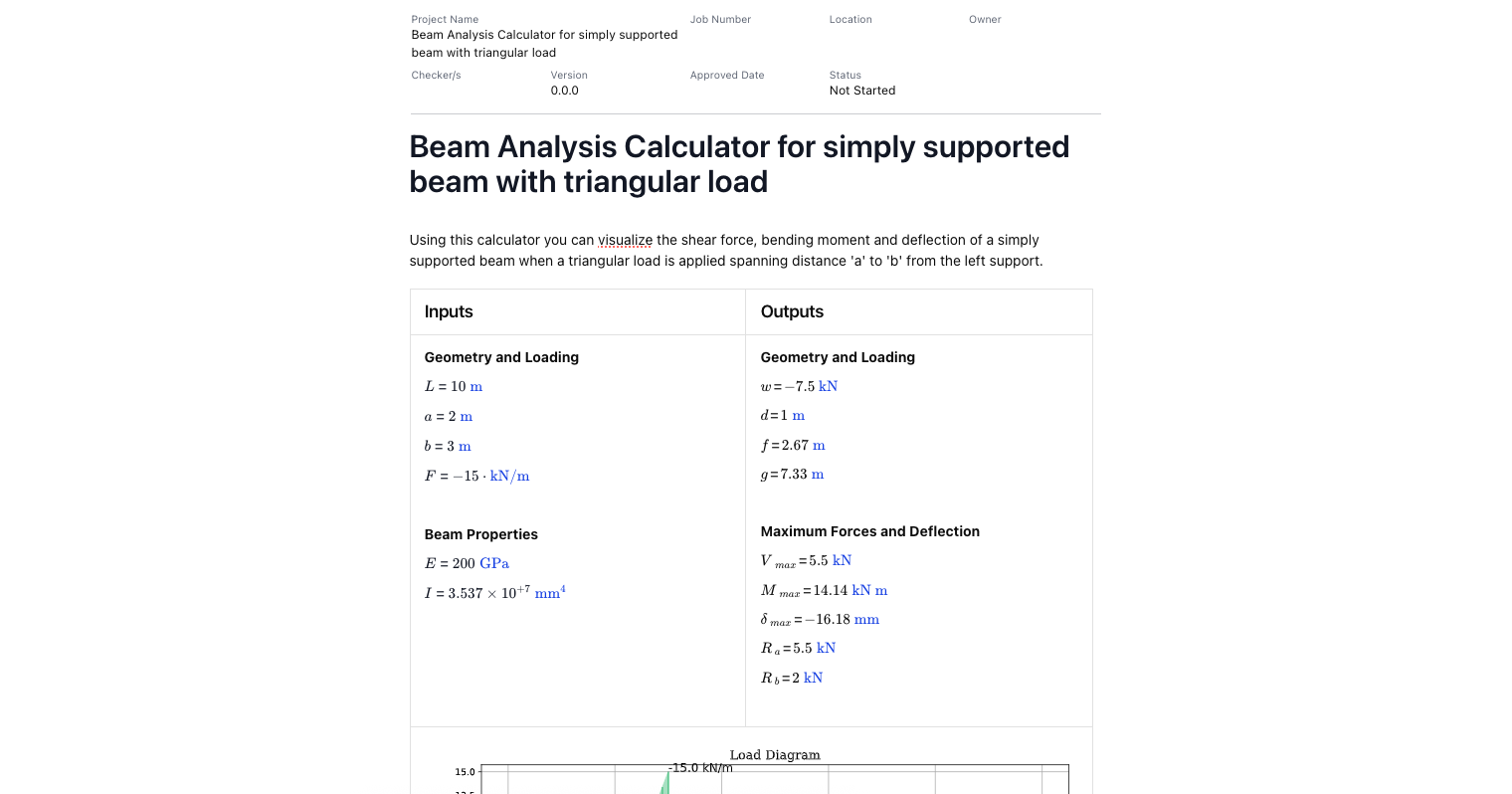
- Simply supported beam with triangular load
- Simply supported beam with trapezoidal load
- Cantilever beam with point moment
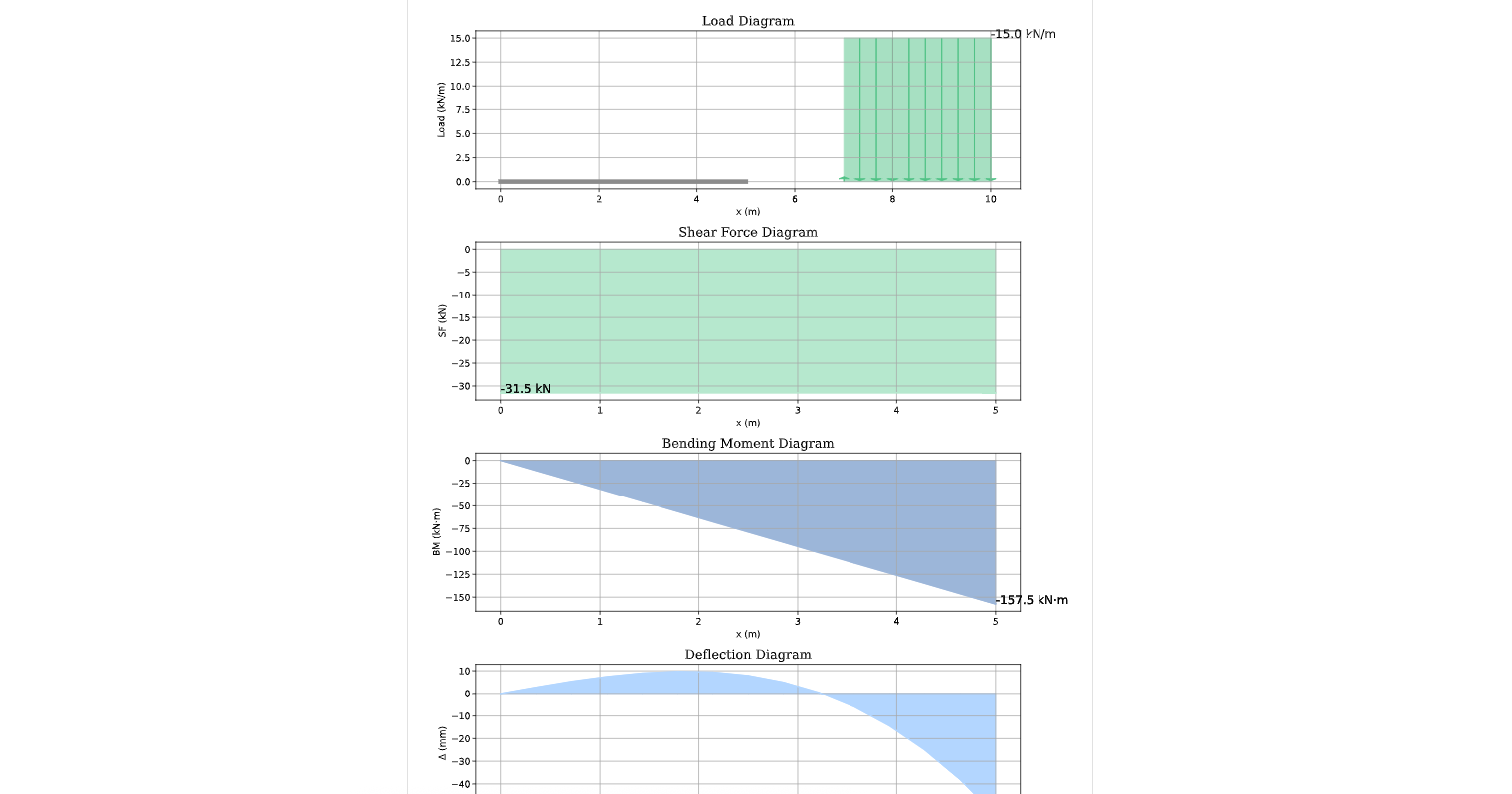
- Cantilever beam with UDL
- Cantilever beam with triangular load
- Cantilever beam with trapezoidal load
By applying Macaulay’s method, the calculators handle step-by-step beam analysis with engineering-grade accuracy, ensuring you can quickly derive a continuous expression for your loaded beam.
General info on Beam Analysis using Macaulay's Theorem
Macaulay’s Theorem Basics
Macaulay’s theorem simplifies the integration of bending moment equations across different spans of a loaded beam. Instead of writing separate equations for each segment, Macaulay’s technique uses a unified format with bracket terms that activate once the applied loads or point loads are reached. This leads to a continuous expression for slope and deflection, even when boundary conditions vary.
Application in Beam Theory
Within beam theory, the theorem is especially useful when working with simply supported beams, cantilever beams, and continuous beams. By integrating the moment distribution equation twice, engineers can find both the slope equation and deflection equation. This works well with uniformly distributed loads and uniformly varying loads, as well as concentrated loads placed at specific positions.
Handling Bending Moment and Shear Force
The theorem creates a direct link between applied loads, reaction forces, and the resulting bending moment and shear force diagrams. For each loaded beam, the method helps ensure sign convention is correctly applied, reducing errors when calculating maximum deflection and ensuring compliance with boundary conditions.
Integration and Deflection
Using the double integration method, Macaulay’s theorem provides the elastic curve of the beam. The slope and deflection are found by integrating the bending moment over the second moment of area (I) and Young’s modulus (E). This allows for precise determination of zero deflection points and maximum deflection locations under beam bending.
Common Calculation Errors to Avoid
When performing beam analysis using Macaulay’s theorem, engineers often fall into common traps:
- Ignoring the correct sign convention when transitioning between bending moment and shear force equations.
- Misapplying boundary conditions on simply supported beams or cantilever beams, leading to wrong reaction forces and deflection.
- Forgetting each applied load (including point loads and distributed loads) creates a new bracket term in the Macaulay’s method equation.
- Using incorrect second moment values for different cross sections, which throws off slope and deflection results.
- Failing to consider moment distribution effects on continuous beams, especially when multiple point loads are present.
- Overlooking material properties like shear stiffness and Young’s modulus, which are crucial for accurate structural analysis.
Engineering templates
Common calculators
Design guides
FAQs
How does Macaulay’s theorem simplify beam analysis?
It combines all loading cases into one continuous expression, avoiding the need for separate equations for each span. This makes solving bending moment and deflection more efficient.
Can Macaulay’s theorem handle cantilever beams as well as simply supported beams?
Yes. Whether it’s a cantilever beam, simply supported beam, or a continuous beam, Macaulay’s method adjusts for applied loads and boundary conditions.
What types of loads can be analyzed using this method?
The theorem works for point loads, multiple point loads, distributed loads, and uniformly varying loads, all integrated into one beam analysis.
How do I find the maximum deflection of a beam using this method?
By integrating the bending moment equation twice (the double integration method) and applying correct boundary conditions, you can pinpoint maximum deflection accurately.
Summary
Macaulay’s theorem streamlines beam analysis by turning complex bending moment and shear force problems into manageable integrations. It’s essential for anyone working with structural analysis, beam bending, or advanced beam theory topics. This calculator ensures you work from a continuous expression, account for applied loads, and get clear results for deflection, slope, and bending moment—all in one place.
For more calculation templates and engineering tools, explore the list provided further below.
Learn about the benefits of using CalcTree on engineering projects!