Pulleys System Calculator: Fixed, Moveable, and Compound Systems

About this Pulley System Calculator

The Pulley System Calculator: Fixed, Moveable, and Compound Systems simplifies the process of determining acceleration in various pulley configurations. Pulley systems have been integral to lifting heavy loads and transmitting power for centuries. This tool supports calculations for fixed, movable, and compound pulley setups. The calculator is suited to:

• Mechanical Engineers working on system dynamics, hoist design, or industrial lifting applications.
• Physics Educators and Students exploring the principles of mechanics and applying them to practical problems.
• Industrial Designers  configuring machinery for material handling or load balancing.

Calculating acceleration in pulleys, users can perform quick feasibility checks to determine system dynamics without manually solving complex equations.

Introduction to Pulley Systems

Pulley systems are designed to redirect or distribute force, enabling users to lift heavy loads with less effort. At the heart of these systems are wheels and ropes or belts, which translate input force into motion while offering mechanical advantage. By configuring pulleys in various ways, users can control the trade-off between force and motion.

The three common types of pulley configurations include:

• Fixed Pulley: Redirects force direction without changing its magnitude.
• Movable Pulley: Shares the load with the anchor point, reducing input effort.
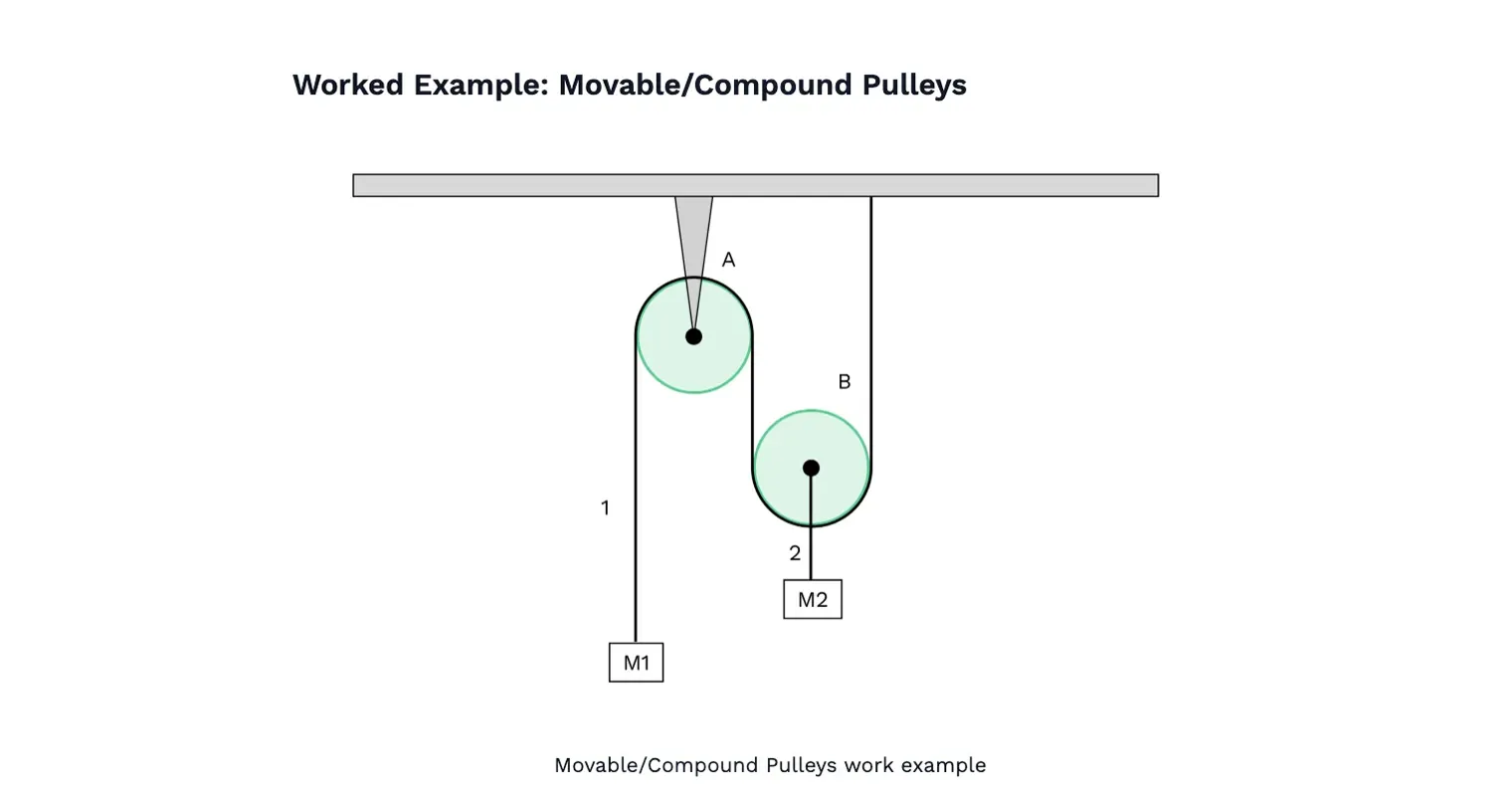
• Compound Pulley (Block and Tackle): Combines fixed and movable pulleys to enhance mechanical advantage.

Each configuration affects system dynamics, including acceleration and effort required. Understanding these distinctions helps users select the most effective arrangement for their application.

Key Components and Forces

An effective pulley system consists of several core components:

• Pulleys (Sheaves): Rotate to guide the rope; can be fixed or movable.
• Rope or Belt: Transmits force and may introduce elasticity or friction.
• Load Mass: The weight being lifted.
• Effort Force: The input applied to move the load.
• Tension: Varies based on pulley configuration and friction.
• Support Structure: Anchors the system and maintains alignment.

Internal forces include tension in the rope, gravitational forces on the masses, and friction at contact points. Each contributes to overall system behavior and must be evaluated for precise analysis.

FAQs

How do fixed, movable, and compound pulleys differ?

Fixed pulleys change the direction of force without altering its magnitude. Movable pulleys reduce the effort required to lift a load. Using two pulleys in a system, such as a block and tackle, further decreases the effort force needed, as the mechanical advantage increases and the effort becomes a smaller fraction of the load. Pulley sets can be configured with multiple ropes and pulleys to maximize mechanical advantage and minimize the force required to lift heavy objects. Compound systems combine both for greater mechanical advantage.

How do you calculate acceleration in a pulley system?

To calculate acceleration, start by applying Newton’s second law to the free-body diagrams of each mass. For a basic two-mass, frictionless pulley system:

$$ a = \frac{(m_2 - m_1)g}{m_1 + m_2}$$

Where \( m_1 \) and \( m_2 \) are the masses, \( g \) is the acceleration due to gravity, and \( a \) is the acceleration.

The process includes:

1. Defining mass and force values
2. Applying the equation above
3. Adjusting for friction and pulley mass
4. Using the calculator to automate complex cases

Can acceleration in pulley systems be affected by friction?

Yes, friction in the pulley and between the rope and pulley surfaces can significantly reduce system efficiency and affect acceleration. Additionally, the angles between the load line and haul line can also impact the mechanical advantage and overall efficiency of the system.

What forces act within a pulley system?

Several forces interact within a pulley system to determine its performance:

• Effort Force: The input force applied by the user or machine to the driver pulley or rope.
• Load Force: The weight of the object being lifted, expressed as mass times gravity.
• Tension: The force transmitted through the rope or belt, which must be equal throughout a frictionless system but can vary with friction or multiple ropes.
• Friction: Resistance between the rope and pulley surfaces, as well as within the pulley bearings, which reduces mechanical efficiency and affects acceleration.
• Gravity: Acts on all masses in the system, influencing the direction and magnitude of forces.

How are pulley systems used in modern applications?

Pulley systems are used in cranes, elevators, conveyor belts, and industrial machinery to lift and move loads efficiently.

Engineers often use a calculator to determine the correct belt length for a pulley system by inputting the pulley diameters and the center-to-center distance (centers) between the pulleys. The calculator can also be used to find the rpm (rotational speed) of both the driver and driven pulleys. By calculating the product of the pulley diameter and rpm, engineers can determine the belt velocity, which is essential for efficient power transmission. Finally, with these parameters, the calculator helps ensure proper alignment and fit, optimizing the performance of the pulley system.

Summary and references

Mastering pulley acceleration is essential in fields ranging from industrial design to physics education. This calculator helps streamline the process by offering a fast, accurate, and accessible way to analyze pulley systems. With support for fixed, movable, and compound setups—and adjustable parameters for friction and load—it serves as a practical engineering resource. For advanced cases involving multiple pulleys or detailed force modeling, refer to simulation tools or engineering textbooks to refine your analysis.

For further study on pulley systems and their principles, consider these references:

• Engineering Mechanics: Dynamics by J.L. Meriam and L.G. Kraige
• Physics for Scientists and Engineers by Raymond A. Serway and John W. Jewett