This tool converts polar coordinates to cartesian coordinates and vice versa. A degree to radian converter (and vice versa) is also provided.
This template is not available yet. You can sign up and create it yourself!
Or let us know if you'd like to be notified when it’s ready:
Your request has been received. We will let you know when it is available.
Oops! Something went wrong while submitting the form.
About this 'Polar to Cartesian Equation Calculator'
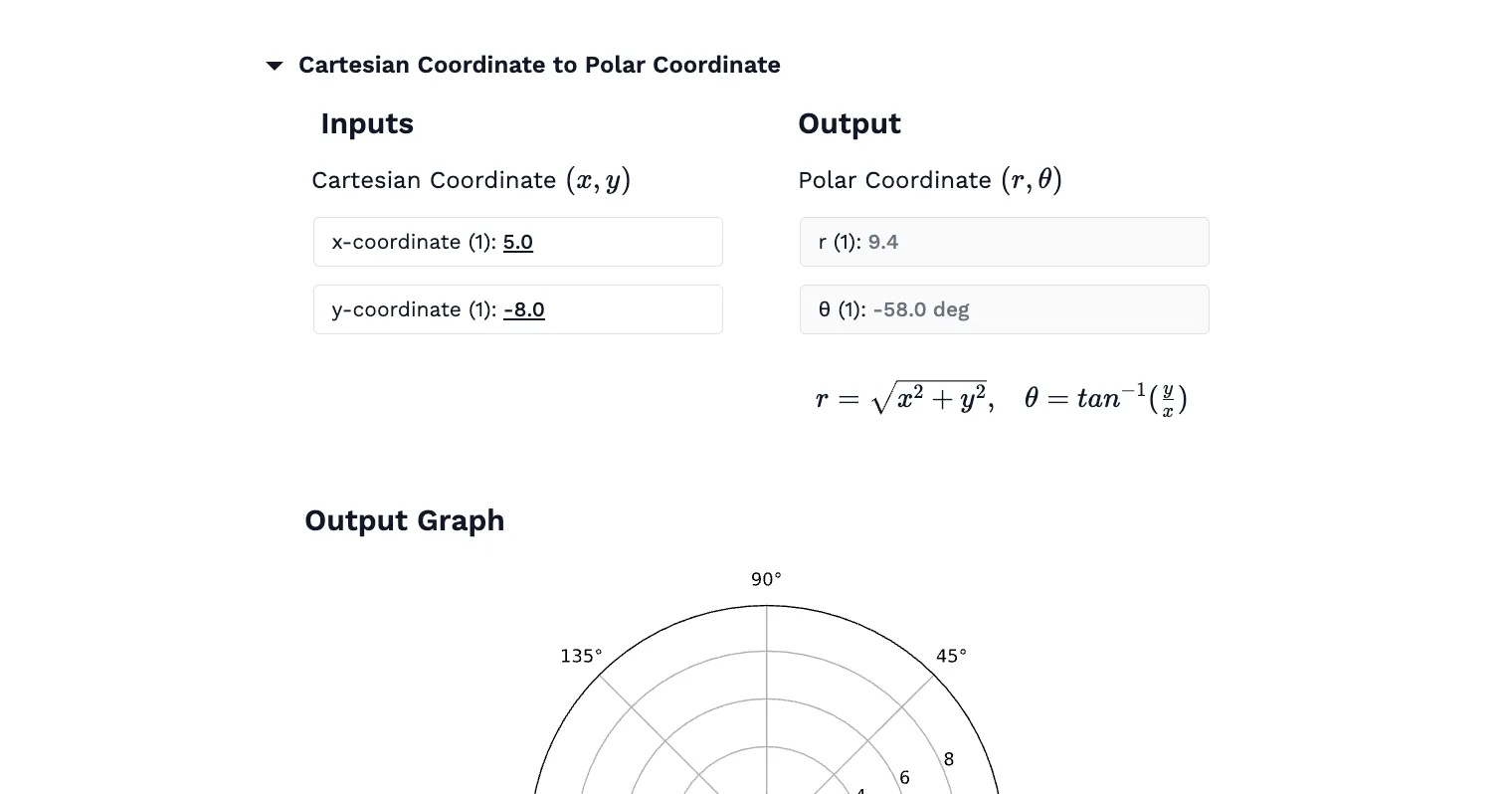
Polar and Cartesian Coordinate Converter is a versatile tool designed to convert between polar and Cartesian coordinate systems. It also includes a degree-to-radian converter (and vice versa), making it an essential resource for applications that involve coordinate transformations, trigonometry, and geometry. Users can enter values for radius and angle, then calculate the corresponding Cartesian or polar coordinates.
This calculator is for:
- Mathematics Students: Understand and practice converting between coordinate systems and learning about their applications in geometry and calculus. Students can choose between degrees and radians when performing conversions.
- Engineers and Scientists: Perform quick conversions to model systems and solve problems involving spatial relationships and trigonometric applications.
- Programmers and Game Developers: Convert coordinates efficiently for tasks like rendering graphics, simulations, and navigation systems.
The Polar to Cartesian Equation Calculator performs fast and accurate conversions, ideal for feasibility checks and classroom use. For more examples and information, visit the Polar Form page. Refer to textbooks such as Advanced Engineering Mathematics by Erwin Kreyszig or Calculus and Analytic Geometry by Thomas and Finney for further reading on these topics.
Introduction to Coordinate Systems
Coordinate systems are essential tools in mathematics and science, providing a way to describe the position of points in a plane or space using numbers. The two most widely used coordinate systems are Cartesian coordinates and polar coordinates, each offering a unique method for representing points and performing calculations.
Cartesian coordinates (also called rectangular coordinates) define a point by its x and y values on two perpendicular axes intersecting at the origin (0, 0). This system is ideal for describing points using linear distances along horizontal and vertical lines and is a foundation of geometry, algebra, and calculus.
Polar coordinates take a different approach. Instead of using two perpendicular axes, polar coordinates describe a point by its distance from the origin (called the radius, r) and the angle (θ) it makes with the positive x-axis, also known as the polar axis. The angle θ can be measured in degrees or radians, and is typically measured counterclockwise from the x-axis. In polar form, a point is represented as (r, θ), where r is the distance from the origin and θ is the angle. This system is especially useful for representing points on a circle, spiral, or any situation where angles and distances from a central point are important.
The ability to convert between polar and Cartesian coordinates is crucial for solving many mathematical problems. The following formulas are used for conversion:
- To convert polar coordinates to Cartesian coordinates: \(x = r cos θ, y = r sin θ\)
- To convert Cartesian coordinates to polar coordinates: \(r = sqrt(x^2 + y^2), θ = arctan(y/x)\)
These formulas allow you to convert polar coordinates into Cartesian values — and convert Cartesian back to polar — giving you flexibility to solve problems in the most convenient form.
It’s important to note that in polar coordinates, the angle θ is not unique—adding or subtracting multiples of 360 degrees (or 2\(π\) radians) will represent the same point. This property can affect how results are interpreted, especially when working with negative values or angles greater than a full rotation.
Understanding both Cartesian and polar coordinate systems, as well as how to convert between them, is fundamental in fields such as trigonometry, calculus, engineering, and physics.
Engineering templates
Common calculators
Design guides
FAQs
How do polar and Cartesian coordinates differ?
Polar coordinates use radius and angle to describe a point, while Cartesian coordinates use x and y values based on perpendicular axes.
What applications use polar coordinates?
Polar coordinates are used in fields like physics, engineering, and computer graphics for modeling circular motion, wave patterns, and rotational systems.
How are polar coordinates applied in navigation?
In navigation, polar coordinates are used to represent the position of an object relative to a reference point, such as a radar system.
Learn about the benefits of using CalcTree on engineering projects!
How to verify a calculation
Engineering calculations require clarity, precision, and professionalism. Here are some best practices we use at CalcTree:
- Technical Requirements: Start with boundary conditions, units, sign conventions, and design standards.
- Check the Math: Review the calculation step-by-step. Clarify unusual steps, compare results with hand calculations or tools, and test with multiple examples.
- Peer Review: Have an independent reviewer check for logic, accuracy, and compliance.
For more on verification, see CalcTree’s internal methods.
